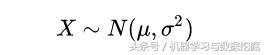在统计学中,一个样本的置信区间是对总体参数的一个区间估计。置信区间给出的是,声称总体参数的真实值在测量值的区间所具有的可信程度或者说是概率。这个概率又叫做置信水平。举例来说:再一次大选中,上帝视角看到某人的支持率是55%,而置信水平0.95上的置信区间是(50%,60%),那么他的真实支持率落在50%到60%之间的概率为95%,如果分布是对称的,那么他支持率不足50%的概率只有2.5%。
对于一个给定的情况,置信水平越高,置信区间就会越大。置信区间表示具体的某个范围,置信水平是一个概率,表示真实值落在这个区间内的概率。
2. 参数估计置信区间属于参数估计中的区间估计
参数估计主要包括点估计和区间估计。其中点估计包括:一阶矩、二阶矩估计、极大似然估计、最小二乘法估计。而置信区间属于区间估计。
3. 置信区间我们通过对人类身高的估计来讲解什么是置信区间。
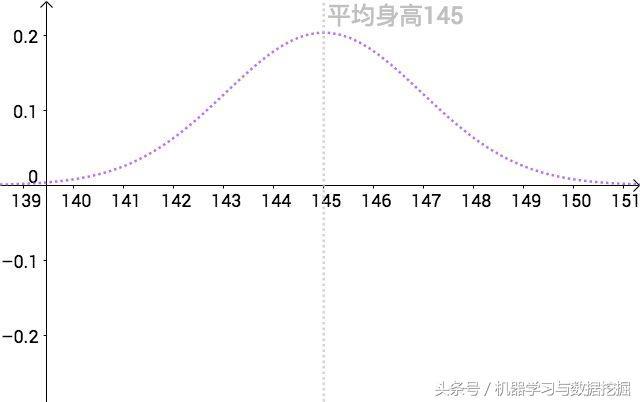
3.1 上帝视角对于人类的平均身高,没有办法全部统计,因为人太多。但是这个数据肯定是真实存在的,我们可以说,上帝知道。也就是说上帝视角可以看到人类身高的真是分布,假设满足正态分布:均值145,标准差1.4.
3.2 点估计
愚蠢的人类想要统计平均身高,没有别的办法,只能进行抽样统计
比如在一次抽样过程中,我们把算出来的样本均值画在图上,蓝色点表示:
那么这个抽样的身高均值就是对真是平均身高的一次点估计。通过一次又一次的抽样,我们可以得到很多个不同的点估计:
现在,关闭上帝视角,根本无法判断哪个点估计更好:
总结:对于点估计来说,直接用样本的均值去估计真实的均值。看上去好像比区间估计要精确。其实不是这样的,如果只用点估计,那么估计正确的概率为0.P(u1 = u) = 0
置信区间虽然依旧不知道哪个估计更好,但是可以给出一个概率。
3.3 置信区间提供的是一种区间估计的办法。不再是直接估计参数的值,而是估计区间包含真实值的概率。比如95%置信区间就是指,给出的这个置信区间有95%的可能会包含真实值。(一般不说:参数的真实值会以95%的概率落在这个区间中。因为参数的真实值不是随机的,他就一个值,而我们的区间才是随机的变化的)。
用点估计给出的估计是X‘ 而用区间估计给出的是区间[X’-1, X’ 1],区间估计估计正确的概率是:
依旧是之前估计人类身高的问题,假设我们用一个固定长度的区间去估计人类身高的均值:
假设选定这个固定长度后,我们抽取不同的样本,得到了不同的估计区间。对于某些抽取的样本来说,估计的区间包含真实值(比如绿色),另一些则不包含(比如红色)。如果在100次的抽取样本实验过程中,有95次构造的估计区间都包含了真实值,那么置信度就为95%。
3.4 置信区间的长度和中点是怎么得到的我们以95%的置信区间来说明
假设人群身高符合正态分布:
其中均值不知道,但是方差已经知道了。目标:估计均值。
我们不断的对人群进行采样,得到了一个大小为n的样本空间,样本的均值为:
那么M也服从于正态分布:
接下来,我们算出以u为中心,面积为0.95的一个区间。在上帝视角看来是这样的:
即:
那现在我们没有办法得到真实的均值。那么只能用抽样样本的均值进行替换了。但是替换之后也出现了一个问题,样本均值和真实值之间存在一定偏差,所以即时区间长度相同,得到的区间也不同。假设我们抽样得到了100个区间,如下图:
可以看到,有的区间包含了真实值,有的区间没有包含真实值。那么100个区间,有多少个包含了真实值那?答案是95%。换个问法:从这100个区间中随机取一个区间,那么包含真实值的概率是多少那?答案是95%。
常见正态分布的图还是可以记一哈:
3.5 如何评价区间估计的好坏
常用的标准有两类:(1)置信度标准 (2)精确度标准
置信度是一个概率,表示估计的区间包含真实值的概率。显然,置信度越大越好。
置信系数是置信度在参数空间上的下边界。因为对于不同的参数,估计出来的置信度不同,显然,我们希望最小的置信度也尽可能的大。所以置信系数越大越好。
精确度标准很多,最常用的是随机区间的平均长度,显然平均长度越小越好。
,