什么是决策树？
决策树模型本质是一颗由多个判断节点组成的树。在树的每个节点做参数判断，进而在树的最末枝(叶结点)能够对所关心变量的取值作出最佳判断。通常，一棵决策树包含一个根结点，若干内部节点和若干叶结点，叶结点对应决策分类结果。分支做判断，叶子下结论。我们看一个简单的决策树的模型，通过动物的一些特点来判断它是否是鱼类，在决策树模型中，我们来看每一个节点是如何做判断的。我们将所有要研究的动物作为树最上端的起点，对它进行第一个判断，是否能脱离水生存？如果判断为是的话，它不是鱼类。如果为否的话，我们还要再进行下一个判断，是否有脚蹼？如果是的话，它就是非鱼类，如果否的话就是鱼类。
我们仅仅是通过最多两个层次的判断，在树最末端的叶子结点，可以对我们感兴趣的问题给出了一个相对而言的最佳决策。这个就是决策树的逻辑，非常简单且和人脑理解事物的逻辑很类似。
决策树是一种简单高效并且具有强解释性的模型，广泛应用于数据分析领域。

• 简单：逻辑相对简单，整个算法没有更复杂的逻辑，只是对节点进行分叉；
• 高效：模型训练速度较快；
• 强解释性：模型的判断逻辑可以用语言清晰的表达出来，比如上述决策树案例中的判断，就可以直接用语言表述成：脱离水不能生存的没有脚蹼的动物，我们判断它是鱼；

决策树模型应用于数据分析的场景主要有三种：

• 监督分层；
• 驱动力分析：某个因变量指标受多个因素所影响，分析不同因素对因变量驱动力的强弱（驱动力指相关性，不是因果性）；
• 预测：根据模型进行分类的预测；

熵是什么？

熵是描述判断的不确定性，大多数决策树的最终判断，并不是100%准确，决策树只是基于不确定性，作出最优的判断。比如上述决策树案例，我们判断脱离水依然可以生存的是“非鱼类”。但是有一种特殊的鱼叫做非洲肺鱼，它脱离水后依然可以存活4年之久。虽然不是100%正确，我们在这个叶结点做出非鱼类的判断，是因为所有脱离水依然可以生存的动物里，有非常大部分都不是鱼。虽然这个判断有很大可能性是正确的，但判断依然存在着一些不确定性。那么不确定性指的是什么呢？如下图，女生占比为50%，具有最大的不确定性；女生占比0%或者100%，则具备最小的不确定性。女生占比30%，具有中等不确定性；如果女性占比为70%的话，我们这个时候猜测是女性，出错可能性是1-70%，即30%，和刚刚的情况相同。也就是说，10个人中女性占比为30%，或是70%，我们虽然给出的判断不同，但是两个判断出错的可能性是一样的，都是30%；图：在10个人中，判断随机挑选出来一个人，性别是男还是女
如果尝试使用一个统计量E来表示不确定性的话，并且规定E的取值在0和1之间。他和人群中女性的占比应该满足这样一条曲线的关系，当女性占比为0或者100%的时候，进行判断的不确定性最小；E取最小值0当女性占比为50%的时候，判断的不确定性最大，E取最大值1；当女性占比取0到50%，或者50%到100%之间的值的时候，E的取值介于0到1之间。并且取值相对女性占比50%是对称的。熵即是用来描述以上这种不确定性，它的数学表达式为：
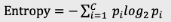
Pi含义：对于事件，有c种可能的结果，每一种可能结果的概率为P1、P2…Pc；熵的取值在0-1之间；一个判断的不确定性越大，熵越大；

信息增益

信息增益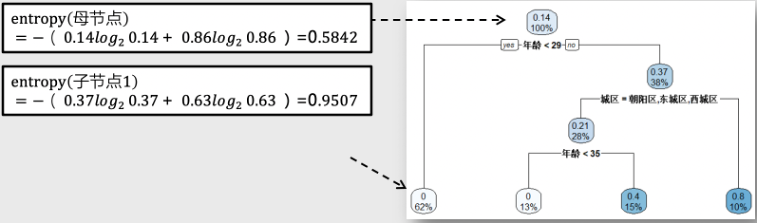表示经过一次决策判断(分叉)后，人群熵值下降的大小，即母节点的熵与两个子节点熵值和的差值。

如上图，信息增益(IG) = 0.5842 - ( 38% * 0.9507 + 62 * 0 )=0.22

决策树算法实现步骤

我们继续用上一篇文章《如何用线性回归模型做数据分析》中的共享单车服务满意分数据集来做案例，分析哪一类人群更加偏向于成为公司的推荐者，我们需要分析用户特征，更好的区分出推荐者。

4.1测量节点对应人群的熵决策树模型的第一步，是测量每个节点对应人群的熵值，最终我们得到可以判断推荐者的决策树。如下图，每个节点中标注两个数字，上面是推荐者比例，下面是用户群占比。初始节点的推荐者比例为0.14，再没任何分叉前，人群占比100%。我们用熵来度量每个节点对应人群的不确定性，推荐者比例趋近0%和100%的人群，熵的值也趋近于0，推荐者比例趋近50%的人群，熵的值则趋近于1。在这个案例中，我们想知道哪一类人更加偏向成为公司的推荐者，也就是说，我们希望通过决策树，可以尽量地划分出是或者不是推荐者这个事情最为确定的人群。如果这样的人群在树的最终结点、也就是叶子结点可以被很好地划分出来的话，那么叶子结点所对应的人群的特征，就是推荐者或者非推荐者的典型特征。反应在人群的熵值计算，更大的确定性对应于比较小的熵值。我们实际上是希望通过决策树不断地分叉，使得节点的熵值越来越低，用户的label越来越纯。4.2节点的分叉-信息增益

我们使用信息增益(IG)来判断决策树的分叉方式。节点分叉规则：在每个节点尝试按照不同特征变量的各种分组方式，选取信息增益最大（熵最小）的方式。
4.3在特定情况树节点停止分叉决策树不会一直不停分叉，决策树停止分叉的条件通常有：

• 树的深度 — 如规定树的深度不能超过3

• 叶子结点样本数 — 如叶子结点样本数不能小于10

• 信息增益 — 如每一个分叉的信息增益不能小于0.2（R中的默认值）

停止分叉：再分叉会增加复杂度但是效果没有提高，叶子越多越复杂，会加重解释复杂性。

决策树在数据分析中的实战流程

我们了解了决策树模型的算法原理，那么它如何应用在日常的数据分析工作中呢？继续我们刚才的案例，我们想探究分析用户推荐程度的主要影响因素是什么？可以用决策树模型将用户按照推荐者比例高低进行分层。一百条数据，由公司员工随机采访100名用户产生，采访对象是北京市四个城区（西城区、东城区、海淀区、朝阳区）的居民，组别分为实验组和对照组。
5.1导入数据集5.2切割自变量和因变量


5.3将分类变量转换为哑变量
Python大多数算法模型无法直接输入分类变量

5.4训练模型

圈出叶子点-最终划分出的人群分层

5.5分析结果
通过人群特征取值的判断，1、我们划分出了推荐者比例有显著区别的人群2、找出了区分推荐者人群的关键特征，例如：海淀区用户、29岁及以上等‘5.6决策树扩展

• 模型建立后，可以将模型用作分类预测；
• 决策树不只可应用于预测量为分类变量，还可应用于数值型因变量，只需将熵改为连续变量的方差；
• 特征划分的方法除了信息增益方法外，还可以用增益率(**.5决策树)、基尼指数(CART决策树)；
• 剪枝是决策树算法中防止过拟合的主要手段，分为预剪枝与后剪枝。预剪枝指在决策树生成过程中，对每个结点在划分前进行估计，若当前结点划分不能使决策树泛化能力提升则停止划分。后剪枝指先从训练集生成一颗决策树，自底向上对非叶结点进行考察，若该结点对应的子树替换为叶结点能使决策树泛化能力提升，则该子树替换为叶结点；